本篇博客文章主要对官方文档做一个翻译,如果有英语基础的小伙伴,可以直接看官方文档。如果有小伙伴对翻译后的内容有质疑,欢迎沟通交流[email protected]
由于官方文档编写过早,在后续rust版本更新和nalgebra库更新,致使一些代码有Bug,我在翻译时会首先将代码跑通,然后只上传正确的代码和文档,对于官方文档中未及时更新的地方,恕不一一指出,这里给出我测试官方文档中代码时的版本:
rust- rustc 1.72.0 (5680fa18f 2023-08-23)nalgebra- 0.32.3
1. 开始
在Cargo.toml文件中加入:
[dependencies]
nalgebra = "*" # replace * by the latest version of the crate.在需要使用nalgebra库的文件头部导入:
use nalgebra as na;1.1 nalgebra库用途及特点
nalgebra是一个整体模块,所有功能都在其内部包根节点导出。不采取多种输参方式的type,traits和functions都可以通过nalgebra::直接导入(如果使用了alias,那么可以直接通过na::导入)。
2. 向量和矩阵
2.1 通用矩阵类型
nalgebra使用相同的通用矩阵架构来表示任意维度的矩阵和向量(在编译或者运行时可知大小)。从本质上讲,向量属于行或者列为一维的矩阵。但为了方便使用,nalgebra给不同类型矩阵取用了不同的alias。
SMatrix<T, R, C>静态矩阵,T指类型,R,C分别代表行列,eg SMatrix<f64,3,4>SVector<T, D>静态向量,T指类型,D代表大小,eg SVector<f64,10>DVector<T>,DMatrix<T>分别代表动态大小的向量和矩阵
同时,nalgebra还为小纬度的静态矩阵和向量也取了别名,方便使用:
Vector1<T> ... Vector6<T>, 分别代表大小从1到6变化的静态列向量RowVector1<T> ... RowVector6<T>, 分别代表大小从1到6变化的静态行向量Matrix1<T> ... Matrix6<T>, 分别代表大小从1到6变化的静态方阵MatrixIxJ<T>, I , J = 1..=6, 可代表I✖️J静态矩阵
以上别名的原型为:Matrix<T, R, C, S>,前三个泛型参数已经介绍,S代表矩阵的可容纳大小,也即capacity。矩阵的大小是否可在编译是可知取决于R和C是否可在编译时可知。
对于程序中经常使用到的矩阵类型,可以给他们创建alias,以避免代码冗余:
use na::{U2, U3, Dynamic, ArrayStorage, VecStorage, Matrix};
type Matrix2x3f = SMatrix<f32, 2, 3>;
// Half-dynamically sized and dynamically allocated matrix with
// two rows using 64-bit floats.
//
// The `OMatrix` alias is a matrix that owns its data (as opposed to
// matrix view which borrow their data from another matrix).
type Matrix2xXf64 = OMatrix<f64, U2, Dynamic>;
// Dynamically sized and dynamically allocated matrix with
// two rows and using 32-bit signed integers.
type DMatrixi32 = OMatrix<i32, Dynamic, Dynamic>;
// Statically sized and statically allocated 1000x3 matrix using 32-bit floats.
type Matrix1000x3f = SMatrix<f32, 1000, 3>;内部实现上,动态矩阵和静态矩阵采取不同的数据存储方式。动态矩阵使用Vec在堆上分配内存;静态矩阵由列优先的2d数组组合而成,具备更好的性能。
2.2 矩阵的构造
所有静态矩阵都可以使用new方法通过行接行的方式来初始化:
// A vector with three components.
let v = Vector3::new(1, 2, 3);
// A matrix with three lines and four columns.
// We chose values such that, for example, 23 is at the row 2 and column 3.
let m = Matrix3x4::new(11, 12, 13, 14,
21, 22, 23, 24,
31, 32, 33, 34);其他构造方法如下:
| Method | Description |
|---|---|
| ::from_rows(…) | Creates a matrix filled with the given array of rows. Panics if any two rows provided do not have the same size. |
| ::from_columns(…) | Creates a matrix filled with the given array of columns. Panics if any two columns provided do not have the same size. |
| ::from_diagonal(…) | Creates a diagonal matrix with its diagonal equal to the provided vector. All off-diagonal elements are set to 0. |
| ::repeat(…) | Creates a matrix filled with the given element (same as ::from_element(…)). |
| ::from_element(…) | Creates a matrix filled with the given element (same as ::repeat(…)). |
| ::from_iterator(…) | Creates a matrix filled with the content of the given iterator. The iterator must provide the matrix components in column-major order. |
| ::from_row_slice(…) | Creates a matrix filled with the content of the given slice. Elements of the slice are provided in row-major order (which is the usual mathematical notation.) |
| ::from_column_slice(…) | Creates a matrix filled with the content of the given slice. Elements of the slice are provided in column-major order. |
| ::from_vec(…) | Creates a matrix filled with the content of the given Vec. Elements of the vec are provided in column-major order. Constructing a dynamically-sized matrix this way consumes the vec to avoid allocations. |
| ::from_fn(…) | Creates a matrix filled with the values returned by the given closure of type FnMut(usize, usize) -> T. This closure is called exactly once per matrix component and is given as parameter each matrix component’s 0-based indices. |
| ::identity(…) | Creates a matrix with 1 on its diagonal and 0 elsewhere. If the matrix to be constructed is not square, only the largest square submatrix formed by its first rows and columns is set to the identity matrix. All the other components are 0. |
| ::from_diagonal_element(…) | Creates a matrix with its diagonal filled with the given element and 0 elsewhere. If the matrix to be constructed is not square, only the largest square submatrix formed by its first rows and columns is set to the identity matrix. All the other components are set to 0. |
| ::new_random(…) | Creates a matrix with all its components initialized at random using the default random generator of the rand crate, i.e., the rand::random() function. |
可以根据代码实例来理解这些函数
fn test_nalgebra() {
use na::{DMatrix, Matrix2x3, RowVector3, Vector2};
use nalgebra as na;
// All the following matrices are equal but constructed in different ways.
let m = Matrix2x3::new(1.1, 1.2, 1.3, 2.1, 2.2, 2.3);
let m1 = Matrix2x3::from_rows(&[
RowVector3::new(1.1, 1.2, 1.3),
RowVector3::new(2.1, 2.2, 2.3),
]);
let m2 = Matrix2x3::from_columns(&[
Vector2::new(1.1, 2.1),
Vector2::new(1.2, 2.2),
Vector2::new(1.3, 2.3),
]);
let m3 = Matrix2x3::from_row_slice(&[1.1, 1.2, 1.3, 2.1, 2.2, 2.3]);
let m4 = Matrix2x3::from_column_slice(&[1.1, 2.1, 1.2, 2.2, 1.3, 2.3]);
let m5 = Matrix2x3::from_fn(|r, c| (r + 1) as f32 + (c + 1) as f32 / 10.0);
let m6 = Matrix2x3::from_iterator([1.1f32, 2.1, 1.2, 2.2, 1.3, 2.3].iter().cloned());
assert_eq!(m, m1);
assert_eq!(m, m2);
assert_eq!(m, m3);
assert_eq!(m, m4);
assert_eq!(m, m5);
assert_eq!(m, m6);
// All the following matrices are equal but constructed in different ways.
//
// This time, we used a dynamically-sized matrix so we must specify the
// dimensions of the matrix with the first two arguments.
let dm = DMatrix::from_row_slice(
4,
3,
&[1.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0],
);
let dm1 = DMatrix::from_vec(
4,
3,
vec![1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0],
);
let dm2 = DMatrix::from_diagonal_element(4, 3, 1.0);
let dm3 = DMatrix::identity(4, 3);
let dm4 = DMatrix::from_fn(4, 3, |r, c| if r == c { 1.0 } else { 0.0 });
let dm5 = DMatrix::from_iterator(
4,
3,
[
// Components listed column-by-column.
1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0,
]
.iter()
.cloned(),
);
// Here is a dynamically-sized vector. The first constructor argument specifies its number of elements.
// let dm1 = DMatrix::from_vec(4, 1, vec![1.0, 2.0, 3.0, 4.0]);
assert_eq!(dm, dm1);
assert_eq!(dm, dm2);
assert_eq!(dm, dm3);
assert_eq!(dm, dm4);
assert_eq!(dm, dm5);
}
编译时大小已知的矩阵也实现了 num crate 中的一些构造traits
| Trait method | Description |
|---|---|
| Zero::zero() | Creates a matrix filled with zeros. |
| One::one() | Creates a matrix with a diagonal set to 1 and off-diagonal elements set to 0. |
| Bounded::min_value() | Creates a matrix filled with the minimal value of the matrix scalar type. |
| Bounded::max_value() | Creates a matrix filled with the maximal value of the matrix scalar type. |
长度 1 到 6 的列向量(只是具有单列的矩阵)具有额外的构造函数:
:x()、::y(), ::z()创建一个向量,分别将第一个、第二个或第三个坐标设置为 1,并将其他坐标设置为 0。::w(), ::a(), ::b()创建一个向量,分别将第四个、第五个或第六个坐标设置为 1,将所有其他坐标设置为 0。
assert_eq!(Vector3::x(), Vector3::new(1.0, 0.0, 0.0));
assert_eq!(Vector3::y(), Vector3::new(0.0, 1.0, 0.0));
assert_eq!(Vector3::z(), Vector3::new(0.0, 0.0, 1.0));
assert_eq!(Vector6::w(), Vector6::new(0.0, 0.0, 0.0, 1.0, 0.0, 0.0));
assert_eq!(Vector6::a(), Vector6::new(0.0, 0.0, 0.0, 0.0, 1.0, 0.0));
assert_eq!(Vector6::b(), Vector6::new(0.0, 0.0, 0.0, 0.0, 0.0, 1.0));向这些构造函数添加 _axis 后缀,例如 ::y_axis(),将创建一个包装到 Unit 结构中的单位向量。例如,Vector2::y_axis() 将创建一个 Unit<Vector2
assert_eq!(Vector6::<i32>::x_axis().into_inner(), Vector6::x());
assert_eq!(Vector6::<u32>::y_axis().into_inner(), Vector6::y());
assert_eq!(Vector6::<f32>::z_axis().into_inner(), Vector6::z());
assert_eq!(Vector6::<f64>::w_axis().into_inner(), Vector6::w());
assert_eq!(Vector6::<u64>::a_axis().into_inner(), Vector6::a());
assert_eq!(Vector6::<i64>::b_axis().into_inner(), Vector6::b());2.3 矩阵操作符
只有两个类型兼容的矩阵才可以进行加、减、乘,除等运算,同时矩阵大小还必须符合矩阵的运算规则。以上检查根据矩阵类型,发生在编译时或者运行时,因此对于动态矩阵我们需要更加小心的处理,避免其在运行时出现错误。需要注意的是,参与运算的矩阵只要有一个为动态矩阵,那么在编译时就不会检查。
let a = Matrix2x3::<f64>::zeros();
let b = DMatrix::<f64>::from_element(4, 4, 0.0);
let _ = a * b; // Compiles fine but panics here.执行cargo check会发现代码编译通过,但执行cargo test时,就会产生报错:
thread 'main' panicked at 'Gemv: dimensions mismatch.'矩阵运算返回值的维度是否在编译时可知取决于以下三条规则:
- 如果两个矩阵的维度在编译时已知,则结果的维度在编译时也已知。
- 如果两个矩阵的维度仅在运行时可知,则返回值矩阵的维度也只能在运行时可知
- 如果一个静态矩阵和动态矩阵相加减,那么返回矩阵的维度在编译时就可知,与静态矩阵的维度相同;如果一个2$\times$3的矩阵和一个动态矩阵相乘,那么返回矩阵的行维度在编译时可知,为2;如果一个2$\times$3矩阵和一个行动态,但列为3的动态矩阵相乘,那么返回矩阵的维度在编译时可知,为2$\times$3。
2.4 改变矩阵中元素的值
当矩阵被声明为mutable时,可以改变矩阵的值,nalgebra库给出了改变矩阵某个元素或者某行某列元素的方法。
let mut m = Matrix3x4::new(11, 12, 13, 14,
21, 22, 23, 24,
31, 32, 33, 34);
m[(0, 2)] = -13;
assert_eq!(m, Matrix3x4::new(11, 12, -13, 14,
21, 22, 23, 24,
31, 32, 33, 34));
m.set_column(1, &Vector3::new(-12, -22, -32));
assert_eq!(m, Matrix3x4::new(11, -12, -13, 14,
21, -22, 23, 24,
31, -32, 33, 34));
m.set_row(2, &RowVector4::new(-31, -32, -33, -34));
assert_eq!(m, Matrix3x4::new(11, -12, -13, 14,
21, -22, 23, 24,
-31, -32, -33, -34));2.5 矩阵切片(官方为Matrix Views)
Matrix Views允许我们获得一个矩阵任意部分的引用。一个Matrix View不会对内存执行任何复制、移动或者分配。Matrix View存储了指向矩阵数据的指针以及有关矩阵大小等信息的元数据。笔者认为,Matrix Views是对矩阵引用的一种继承类型,它本质上就是引用,但提供了很多函数,便于我们精确获取矩阵中某些数据。
以下三种情况不可使用Matrix Views:
- Matrix Views不能调用传入&mut self参数的函数
- Matrix Views只能从已有矩阵中创建,不可凭空生成
- Matrix Views不能进行赋值操作。
时刻牢记Matrix Views只是一个&Matrix类型,那么以上三条规则就很容易理解。至于引用的生命周期,我猜测在内部实现上应该使用了共享指针,否则很容易出现引用生命周期的问题,感兴趣的小伙伴可以自行查阅源码。
同样的,Matrix Views类型也分为Fixed Views、Dynamic Views和Stride Views。
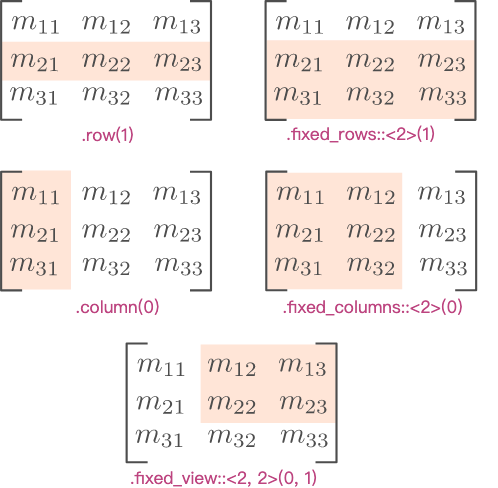
Fixed Views
指编译时可知大小的Matrix Views,相关的方法名称一般以fixed开头
| Method | Description |
|---|---|
| .row(i) | Reference to the i-th row of self. |
| .column(i) | Reference to the i-th column of self. |
| .fixed_rows:: |
Reference to the submatrix with D consecutive rows of self, starting with the i-th. D must be an integer. |
| .fixed_columns:: |
Reference to the submatrix with D consecutive columns of self, starting with the i-th. D must be an integer. |
| .fixed_view::<R, C>(irow, icol) | Reference to the submatrix with R consecutive rows and C consecutive columns, starting with the irow-th row and icol-th column. R and C are integers. |
Dynamic Views
指大小在运行期间才可知的矩阵
| Method | Description |
|---|---|
| .rows(i, size) | Reference to size rows of self, starting with the i-th. |
| .columns(i, size) | Reference to size columns of self, starting with the i-th. |
| .view(start, shape) | Reference to the submatrix with shape.0 rows and shape.1 columns, starting with the start.0-th row and start.1-th column. start and shape are both tuples. |
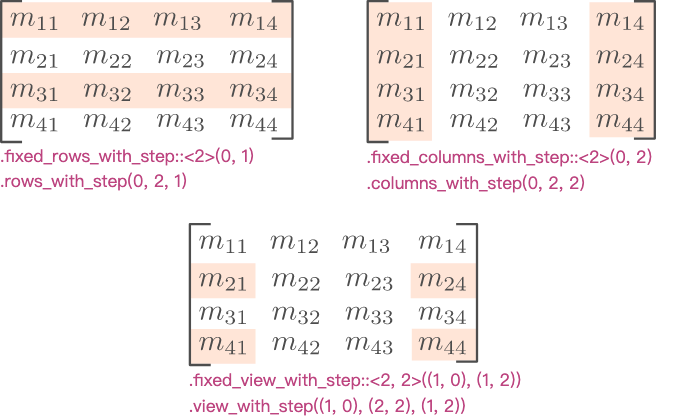
Strides Views
Strides Views允许你设定步长来获取矩阵的引用
| Method | Description |
|---|---|
| .fixed_rows_with_step:: |
Reference to D non-consecutive rows of self, starting with the i-th. step rows of self are skipped between each referenced row. |
| .fixed_columns_with_step:: |
Reference to D non-consecutive columns of self, starting with the i-th. step columns of self are skipped between each referenced column. |
| .fixed_view_with_steps::<R, C>(start, step) | Reference to R and C non-consecutive rows and columns, starting with the component (start.0, start.1). step.0 (resp. step.1) rows (resp. columns) are skipped between each referenced row (resp. column). |
| .rows_with_step(i, size, step) | Reference to size rows of self, starting with the i-th. step rows are skipped between each referenced row. |
| .columns_with_step(i, size, step) | Reference to size columns of self, starting with the i-th. step columns are skipped between each reference column. |
| .view_with_steps(start, shape, steps) | Reference to shape.0 rows and shape.1 columns, starting with the (start.0, start.1)-th component. step.0 (resp. step.1) rows (resp. columns) are skipped between each referenced row (resp. column). |
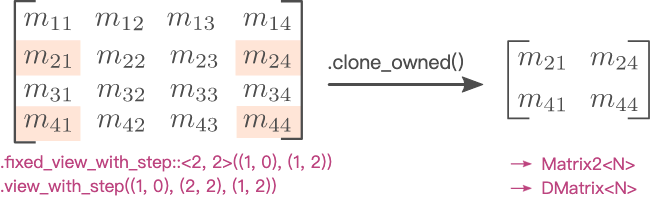
.clone_owned()用于从一个Matrix View创建具备所有权的矩阵
2.6 改变矩阵的大小
矩阵的行数或列数可以通过添加或删除其中一些来修改。与Matrix Views类似,存在两种类型:
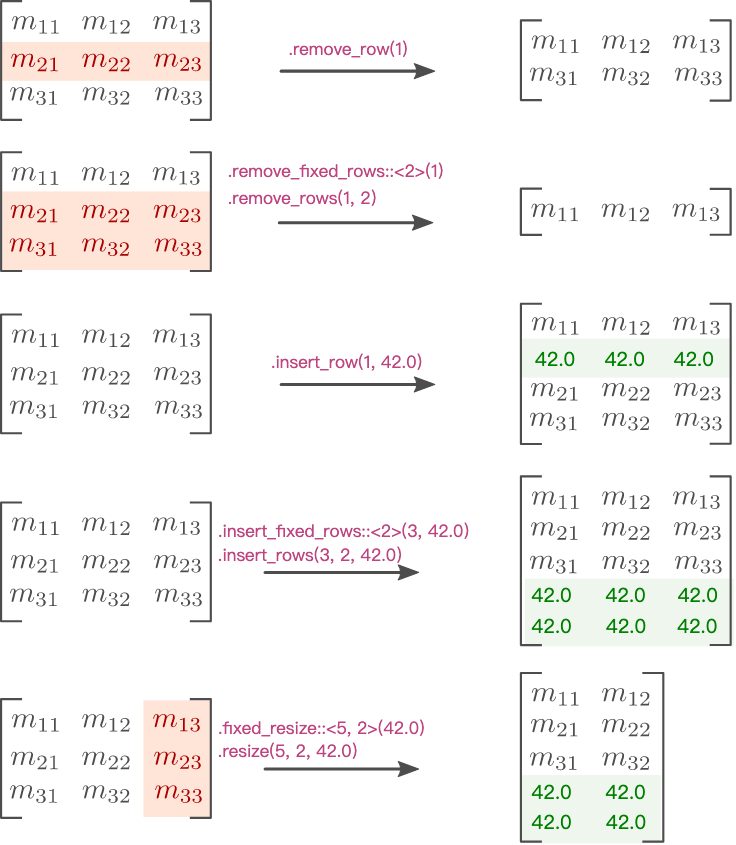
Fixed resizing
其中要删除或插入的行数或列数在编译时已知。当输入也是静态大小时,输出也是静态大小的矩阵。
| Method | Description |
|---|---|
| .remove_row(i) | Removes the i-th row. |
| .remove_column(i) | Removes the i-th column. |
| .remove_fixed_rows:: |
Removes D consecutive rows, starting with the i-th. |
| .remove_fixed_columns:: |
Removes D consecutive columns, starting with the i-th. |
| .insert_row(i, val) | Adds one row filled with val at the i-th row position. |
| .insert_column(i, val) | Adds one column filled with val at the i-th row position. |
| .insert_fixed_rows:: |
Adds D consecutive rows filled with val starting at the i-th row position. |
| .insert_fixed_columns:: |
Adds D consecutive columns filled with val starting at the i-th column position. |
| .fixed_resize::<R2, C2>(val) | Resizes the matrix so that it contains R2 rows and C2 columns. Components are copied such that result[(i, j)] == input[(i, j)]. If the result matrix has more rows or more columns, then the extra components are initialized to val. |
Dynamic resizing
其中要删除或插入的行数或列数在编译时未知。结果矩阵将始终动态调整大小(Matrix<…> 维度相关类型参数被设置为 Dynamic)。
| Method | Description |
|---|---|
| .remove_rows(i, n) | Removes n rows, starting with the i-th. |
| .remove_columns(i, n) | Removes n columns, starting with the i-th. |
| .insert_rows(i, n, val) | Inserts n rows filled with val starting at the i-th row position. |
| .insert_columns(i, n, val) | Inserts n columns filled with val starting at the i-th row position. |
| .resize(new_nrows, new_ncols, val) | Resizes the matrix so that it contains new_nrows rows and new_ncols columns. Components are copied such that result[(i, j)] == input[(i, j)]. If the result matrix has more rows or more columns, then the extra components are initialized to val. |
以上函数传入的隐式参数均为self,转移所有权的目的是为了得到有所有权的结果。无论待增加/减少的行/列是否在编译时可知,都可使用fixed resizing。
强烈建议在可能的情况下都使用fixed resizing,尤其是当被改变大小的矩阵为静态矩阵时。实质上,dynamic resizing涉及到在堆上的内存读写和分配,会导致程序性能降低。